


LOGARITHMS

Java provides us with only one method for working with Logarithms: 
java.lang.Math.log(). It returns the log (base 10) of the number
passed as its argument. In the absence of functions for log base 2 and
log base e, we must create our own. Here's the basic formula:


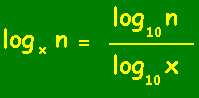
With this information it is not difficult to define methods which
return the log base anything of any number.

A problem occurs, however, when you work with really big numbers (the
kind that require more than 64-bits of memory). Java provides a class
called BigInteger which will deal with these really big numbers, but
it doesn't provide a method to find logarithmic values for these numbers.
So, you've got to come up with a way to find logarithms for really big numbers
on your own.
There are two strategies for dealing with this situation:

1. Calculate the Log Value: 




You will need to experiment with this infinite series to figure out how
far you have to go to get a good approximation of log values (in fact, that's
what your assignment is going to be).
2. Use the Sum of Factors:



If you can factor a very large number into values which can be handled by
a 64-bit long variable, then you can find its sum. I used this strategy in
the example shown below to find the value of n!. Instead of actually calculating
the value of n! and then attempting to determine it's log, I simply calculated
the sum of log 1 + log 2 + log 3 + ... log n.

Example:


import java.awt.*;
import java.awt.event.*;
import java.applet.*;
import java.math.BigInteger;

public class functions extends Applet {

  int n;
  Label [] lab;
  TextField [] tf;
  TextField input;

  public void init() {
    setBackground(Color.yellow);
    setLayout(null);
    lab = new Label[6];
    lab[0]=new Label("log (base 2) n:"); lab[0].setBounds(10,60,80,20);
    lab[1]=new Label("n:");  lab[1].setBounds(10,80,80,20);
    lab[2]=new Label("log (base 2) n!:");  lab[2].setBounds(10,100,80,20);
    lab[3]=new Label("n^2:");  lab[3].setBounds(10,120,80,20);
    lab[4]=new Label("2^n:");  lab[4].setBounds(10,140,80,20);
    lab[5]=new Label("n!:");  lab[5].setBounds(10,160,80,20);
    tf = new TextField[6];
    for(int i=0; i<6; i++) {
      add(lab[i]);
      tf[i]=new TextField();
      tf[i].setBounds(100,60+i*20,300,20);
      add(tf[i]);
    }
    Button b = new Button("Process");
    b.setBounds(10,180, 60,20);
    b.addActionListener(new ActionListener(){
      public void actionPerformed(ActionEvent e) {
        int n=Integer.parseInt(input.getText());
        doTheStuff(n);
      }
    });
    add(b);
    input = new TextField("Enter n here");
    input.setBounds(100, 180, 300, 20);
    doTheStuff(10);
    add(input);
    Label title=new Label("Comparative Growth");
    title.setFont(new Font("Serif", Font.BOLD, 24));
    title.setBounds(30,30,400,25);
    add(title);
  }

  public void doTheStuff(int n){
    tf[0].setText(""+(int)(Math.log(n)/Math.log(2)));
    tf[1].setText(""+n);
    BigInteger fact2 = new BigInteger("1");
    for(int i=1; i<=n; i++) {
      fact2=fact2.multiply(new BigInteger(""+i));
    }
    float seed=0;
    for(int i=1; i<=n; i++) seed+=Math.log(i)/Math.log(2);
    tf[2].setText(""+seed);
    tf[5].setText(""+fact2);
    BigInteger big = new BigInteger("2");
    big=big.pow(n);
    tf[4].setText(""+big);
    tf[3].setText(""+(long)Math.pow(n,2));
  }
}

//<applet code=functions.class height=250 width=500></applet>




Assignment: As mentioned above, you will create an applet which
implements the formula shown above for calculating a log base e value. 
 You will provide one
input textarea and two output textareas. One will show the value generated by
your function using the above equation and the other will show the value 
generated by the log function provided with Java. FYI, java.lang.math provides
a double variable E.