Python Basics and Biostatistics

The Gaussian Distribution

Back to index
In this lesson the student will learn how to:
  1. calculate the z for an individual score
  2. recognize a Gaussian distribution
  3. recognize Python built in functions
By the end of this lesson the student will be able to: 

  Write a script to calculate the z for an individual
  score given the SD and mean for a data set.
The bell-shaped curve was mentioned in the last lesson. This symmetrical bell-shaped distribution is formally called a Gaussian distribution. Data will often approximate a Gaussian distribution when the variation of our data is caused by many different factors. For instance, let's say we where measuring height in a population of adult human females. Since height is a trait influenced by many independent genetic and environmental factors, the heights of the females in our sample will almost certainly approximate a bell-shaped curve (providing that we take random samples from a naturally occurring population).

This is not likely to be the case when variation is largely due to one factor (such as would be the case if the variation were due to only one gene). In this case you expect either a skewed distribution or a bimodal distribution instead of a Gaussian distribution. For instance, imagine that 90% of variation in height could be accounted for by a single gene and that other genes and environmental factors had only a combined effect of 10% on the resulting phenotype observed in individual subjects in our sample. In this case we would quite possibly see a skewed or bimodal plot of our data for adult human female height which might possibly reflect breeding trends which are influenced by various social factors. Since height, however, is acually influenced by many genes and many environmental factors, a Gaussian distribution will almost certainly be reflected in our data.

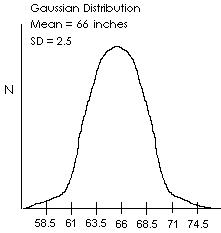
The mean is at the center or peak in a Gaussian distribution. The SD is a measure of the spread of the distribution. The entire population is represented by the area under the curve. Two thirds of the population will be within one SD of the mean. The number of SD's from the mean at which an individual value falls is referred to as that value's z. A z of zero would be the z for a score which equals the mean. The z is calculated using this formula. 


   z = abs(Y - mean) / SD
The abs function is short for absolute value. (For instance, the absolute value for both 5 and -5 is 5 since absolute value refers to the distance of a value from zero.)

As you can see, z is just the number of SD's from the mean of single score.

So, let's say that we have some data with a mean of 66 and a SD of 2.5. Let's say we have an individual with a score of 62 and we want to know the value of z. To find z, we just plug in the numbers like this: 


   z = abs( 62 - 66 ) / 2.5
     = 4 / 2.5
     = 1.6
So, we find that the z for our individual is 1.6 and since our individual is below the mean we could say that our individual score is 1.6 SD's below the mean.

Python Script to Calculate z

As luck would have it (and as you will hopefully recall), Python provides us with a function to find the absolute value of a integer. It's as easy as this:

val = abs(-5) We can also use it for expressions like this: a = 10 b = 5 val = abs(b-a) In both examples val winds up with positive five stored in it.

Python Built In Functions and Math Functions

At this point you have used several built in functions and math functions. Usually you assign the output of a function to a variable like this:

n1 = math.sqrt(81) n2 = abs(x) There are MANY built in functions and math functions which we will be using in the future.

Assignment:

Write a Python script which calculates the z for a score. Your script will take three inputs: 1) mean, 2) SD, and 3) individual score. It will provide output in this form: 


  Mean: 100
  SD: 12.5
  SCORE: 122.5
  z: 1.8