Arithmetic Grade Six

Lesson One Hundred Forty-five: Interior Angles of Quadrilaterals

Angles are measured in degrees (they can also be measured in radians, but we won't deal with radians). A quadrilateral has four vertices and the interior of each vertice forms an angle. The sum of the four interior angles of a quadrilateral is always 360 degrees.

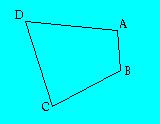
These are the sizes of the angles of the quadrilateral to the right.

  1. 65 degrees
  2. 107 degrees
  3. 115 degrees
  4. 73 degrees
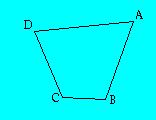
Since we know that the sum of the interior angles of a quadrilateral is always 360 degrees, we can always figure out the size of the fourth angle providing that we know the size of the other three. Consider this example:
  1. 79 degrees
  2. 91 degrees
  3. 101 degrees

The missing angle will equal: 

   360 - 79 - 91 - 101 =
Solving this problem will yield 89 degrees as the size of the missing angle.
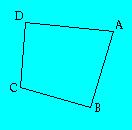
Here's another missing angle for you to figure out:
  1. 100 degrees
  2. 113 degrees
  3. 80 degrees
The solution: 

   360 - 100 - 113 - 80 = 67 degrees

Click here to go to next page