
As you can see there are ten balls and six are yellow and four are red. The probability of reaching in the bag and pulling out a yellow ball is 6 out of 10. The probability of reaching in the bag and pulling out a red ball is 4 out of 10.
Think about flipping a coin for a moment. When you flip a coin it can come up heads or tails. The chances of a coin coming up heads or tails is equal. Before you flip the coin you know that you have an equal chance of it coming up heads or tails. We can say that the probability of the coin coming up heads is equal to the probability of it coming up tails. The probability of an event is the chance that the event will occur.
Let's say that you have a bag containing six stones and that two are painted red and four are painted green. If you reach into the bag and without looking pull out a stone what is the probability of pulling out a red stone? Since there are six stones in the bag and two are red, the probability of pulling out a red stone is 2 out of 6. The probability of pulling out a green stone is 4 out of 6. In other words, you are more likely to pull out a green stone than a red stone (which makes sense since there are more green than red stones in the bag).
The following picture represents a group of ten balls in a bag.

As you can see there are ten balls and six are yellow and four are red. The
probability of reaching in the bag and pulling out a yellow ball is 6 out of
10. The probability of reaching in the bag and pulling out a red ball is 4
out of 10.
Here are ten more balls.
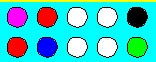
This time we have four white balls, two red balls, and one ball each of
black, green, blue, and magenta. (Magenta is the reddish-purplish color.)
We can answer questions like about this group of balls:
1) What is the probability of pulling out a red ball?
ANSWER: 2 out of 10
2) Which color ball are we most likely to pull out?
ANSWER: white
3) What is the probability of pulling out a ball which is not white or red?
ANSWER: There are four balls that are not white or red.
So, 4 out of 10 is the probability of not pulling
out a ball which is white or red.